Work from the group and collaborators on learning dynamics, bias, curricula, continual learning, optimisation, and statistical physics.
Recent papers and preprints, shown first for a quick view of what is currently moving.
Real-world datasets differ across classes in both structure and frequency, but most theory for diffusion models assumes homogeneous data. This work develops a high-dimensional analytical framework for class-dependent learning in score-based diffusion models. Using...
Open paper
Model collapse can degrade generative models when they are trained on outputs from earlier models. This position paper argues that the problem compounds existing concerns around large language models, including cultural bias, data degradation,...
Open paper
We study the population loss landscape of two-layer ReLU networks in a realisable teacher-student setting with Gaussian covariates. The work shows that local minima admit an exact low-dimensional representation through summary statistics, giving a...
Open paperBrowse the complete list, newest first.
Real-world datasets differ across classes in both structure and frequency, but most theory for diffusion models assumes homogeneous data. This work develops a high-dimensional analytical framework for class-dependent learning in score-based diffusion models. Using a random-features model trained on Gaussian mixtures, the paper characterizes how class...
Open paper
Model collapse can degrade generative models when they are trained on outputs from earlier models. This position paper argues that the problem compounds existing concerns around large language models, including cultural bias, data degradation, environmental cost, and inefficient resource use. The authors highlight how these dynamics...
Open paper
We study the population loss landscape of two-layer ReLU networks in a realisable teacher-student setting with Gaussian covariates. The work shows that local minima admit an exact low-dimensional representation through summary statistics, giving a sharp and interpretable description of the landscape. It also links local minima...
Open paper
This pedagogical paper introduces statistical-physics approaches to machine learning, based on material presented at Analytical Connectionism 2023. It reviews how tools such as the replica method and approximate message passing illuminate unsupervised learning problems, then turns to supervised learning and neural-network dynamics in lazy-learning and feature-learning...
Open paper
Machine learning (ML) may be oblivious to human bias but it is not immune to its perpetuation. Marginalisation and iniquitous group representation are often traceable in the very data used for training, and may be reflected or even enhanced by the learning models. In the present...
Open paper
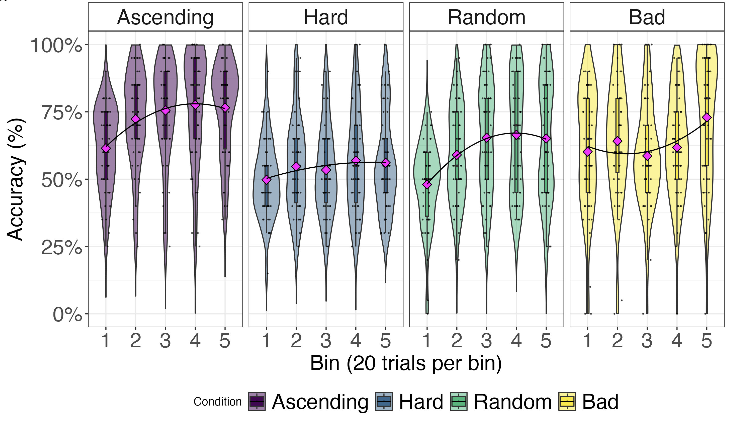
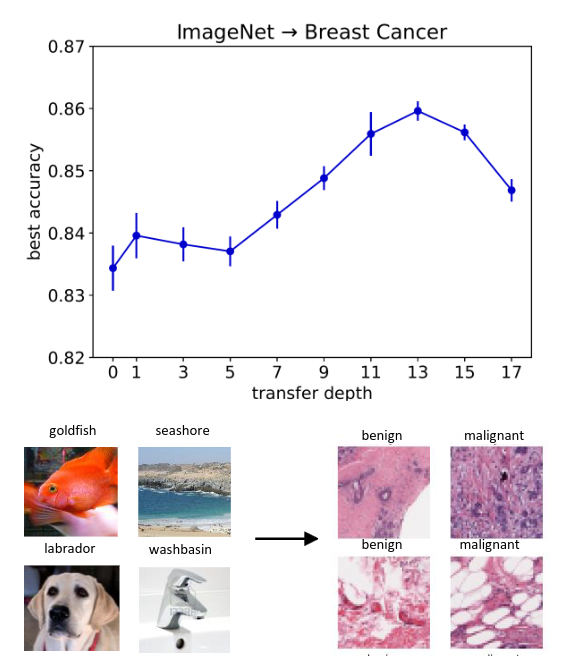
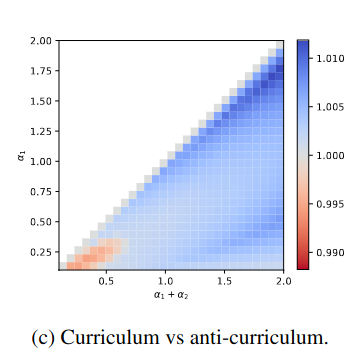
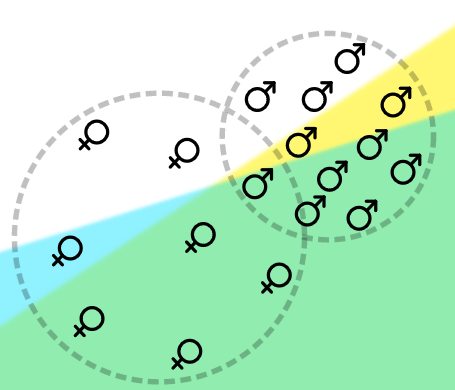
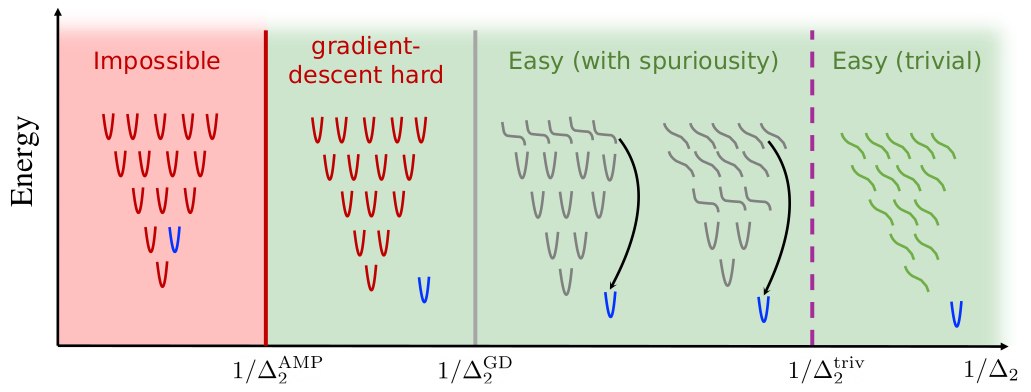
The sequencing of training trials can significantly influence learning outcomes in humans and neural networks. However, studies comparing the effects of training curricula between the two have typically focused on the acquisition of multiple tasks. Here, we investigate curriculum learning in a single perceptual decision-making task,...
Open paper
Prior work has demonstrated a consistent tendency in neural networks engaged in continual learning tasks, wherein intermediate task similarity results in the highest levels of catastrophic interference. This phenomenon is attributed to the network's tendency to reuse learned features across tasks. However, this explanation heavily relies...
Open paper
Artificial neural networks often struggle with catastrophic forgetting when learning multiple tasks sequentially, as training on new tasks degrades the performance on previously learned ones. Recent theoretical work has addressed this issue by analysing learning curves in synthetic frameworks under predefined training protocols. However, these protocols...
Open paper
Transfer learning is a powerful tool enabling model training with limited amounts of data. This technique is particularly useful in real-world problems where data availability is often a serious limitation. The simplest transfer learning protocol is based on ``freezing" the feature-extractor layers of a network pre-trained...
Open paper
The ability to exert cognitive control is central to human brain function, facilitating goal-directed task performance. However, humans exhibit limitations in the duration over which they can exert cognitive control -a phenomenon referred to as cognitive fatigue. This study explores a computational rationale for cognitive fatigue...
Open paper
Machine learning systems often acquire biases by leveraging undesired features in the data, impacting accuracy variably across different sub-populations. Current understanding of bias formation mostly focuses on the initial and final stages of learning, leaving a gap in knowledge regarding the transient dynamics. To address this...
Open paper
A wide range of empirical and theoretical works have shown that overparameterisation can amplify the performance of neural networks. According to the lottery ticket hypothesis, overparameterised networks have an increased chance of containing a sub-network that is well-initialised to solve the task at hand. A more...
Open paper
Diverse studies in systems neuroscience begin with extended periods of training known as 'shaping' procedures. These involve progressively studying component parts of more complex tasks, and can make the difference between learning a task quickly, slowly or not at all. Despite the importance of shaping to...
Open paper
Reinforcement learning (RL) algorithms have proven transformative in a range of domains. To tackle real-world domains, these systems often use neural networks to learn policies directly from pixels or other high-dimensional sensory input. By contrast, much theory of RL has focused on discrete state spaces or...
Open paper
In animals and humans, curriculum learning -presenting data in a curated order- is critical to rapid learning and effective pedagogy. A long history of experiments has demonstrated the impact of curricula in a variety of animals but, despite its ubiquitous presence, a theoretical understanding of the...
Open paper
Continual learning - learning new tasks in sequence while maintaining performance on old tasks - remains particularly challenging for artificial neural networks. Surprisingly, the amount of forgetting does not increase with the dissimilarity between the learned tasks, but appears to be worst in an intermediate similarity...
Open paper
Transfer learning can significantly improve the sample efficiency of neural networks, by exploiting the relatedness between a data-scarce target task and a data-abundant source task. Despite years of successful applications, transfer learning practice often relies on ad-hoc solutions, while theoretical understanding of these procedures is still...
Open paper
The optimization step in many machine learning problems rarely relies on vanilla gradient descent but it is common practice to use momentum-based accelerated methods. Despite these algorithms being widely applied to arbitrary loss functions, their behaviour in generically non-convex, high dimensional landscapes is poorly understood. In...
Open paper
Contact tracing is an essential tool to mitigate the impact of a pandemic, such as the COVID-19 pandemic. In order to achieve efficient and scalable contact tracing in real time, digital devices can play an important role. While a lot of attention has been paid to...
Open paper
We study the dynamics of optimization and the generalization properties of one-hidden layer neural networks with quadratic activation function in the overparametrized regime where the layer width m is larger than the input dimension d. We consider a teacher-student scenario where the teacher has the same...
Open paper
Despite the widespread use of gradient-based algorithms for optimising high-dimensional non-convex functions, understanding their ability of finding good minima instead of being trapped in spurious ones remains to a large extent an open problem. Here we focus on gradient flow dynamics for phase retrieval from random...
Open paper
We review recent works (Sarao Mannelli et al 2018 arXiv 1812.09066, 2019 Int. Conf. on Machine Learning 4333–42, 2019 Adv. Neural Information Processing Systems 8676–86) on analyzing the dynamics of gradient-based algorithms in a prototypical statistical inference problem. Using methods and insights from the physics of...
Open paper
Gradient-descent-based algorithms and their stochastic versions have widespread applications in machine learning and statistical inference. In this work, we carry out an analytic study of the performance of the algorithm most commonly considered in physics, the Langevin algorithm, in the context of noisy high-dimensional inference. We...
Open paper
Gradient-based algorithms are effective for many machine learning tasks, but despite ample recent effort and some progress, it often remains unclear why they work in practice in optimising high-dimensional non-convex functions and why they find good minima instead of being trapped in spurious ones. Here we...
Open paper
In this work we analyse quantitatively the interplay between the loss landscape and performance of descent algorithms in a prototypical inference problem, the spiked matrix-tensor model. We study a loss function that is the negative log-likelihood of the model. We analyse the number of local minima...
Open paperNo publications match this filter.